I need to vent
-
@anluc7 Thanks. I should know better about the “Law of Large Numbers” since I do have an ancient BS in physics and have taught & tutored HS & college math, but I do wonder about how they can guarantee the randomness of the number generator for the dice rolls.
It actually could be tested since the Play-By-Play records each dice roll in a game but it might take a few PhDs in statistics and a super-computer to crunch the numbers.
Anyway, APBA got me through HS in the early 60s and aided and abetted me becoming a stathead for more than baseball.
-
For what it’s worth, I always use the manual dice roll option. It was never because I felt the computer rolls had trends. I’ve just always loved the feel of the dice in my hand when rolling APBA (dating back to 1974).
The thing I really like about GO is not having to cross-reference from dice… to cards… to boards. And then have to take into consideration pitcher grades and fielding ratings. GO does all that instantly. Great entertainment.
But I still like the dice in my hand. :wink: -
@tomfortas-0 Hi!
Dice rolls are done using the Java random number generator function for most dice rolls, unless you use 3D dice, in which case the dice rolls are determined by the physics simulation of how the 3D dice land.
Some things that mess with people’s heads regarding dice rolls:
1,1,1,1,1,1
1,2,3,4,5,6
1,3,5,4,2,6are equally random.
A percentage breakdown of results such as:
1 - 16%
2 - 17%
3 - 12%
4 - 12%
5 - 21.5%
6 - 21.5%after 100 rolls will look like:
1 - 16.67%
2 - 16.67%
3 - 16.67%
4 - 16.67%
5 - 16.67%
6 - 16.67%after a million rolls (or whatever the statistically significant number of rolls required and proper decimal accuracy actually is).
Software random number generators can show flaws if the sample size is large enough, but they pale in comparison to a poorly manufactured die thrown the same number of times (or so I’m told, I’ve never actually done the test myself… although I do feel I own friendly and unfriendly cheap dice).
-
The “random” feature has seemed a little off lately.
I would love to know the odds of the following sequence of rolls that happened in a game over the weekend.
53, 53, 53, 31, 53.I have also seen back-to-back-to-back 11s and 66s in the same game earlier this season. Another time it was 4 straight 46s (two for each team). .
I know each roll has a 1 in 36 chance of happening but it does seem a little strange. Especially when you are on the wrong side of the rolls…
-
@APBA-GO-Jeremy
Hi Jeremy, thanks so much for responding. You covered well the theory behind the law of large numbers in establishing true randomness. (As a retired HS math teacher & tutor, I would like to use your example in giving the students a feel for the “law” since dice rolls are so instructive. Somehow they seemed to grasp the 1 out of 6 possibilities better than the coin-flipping 1 out of 2)However, in APBAGO here, I’m noticing that a number of players are coming up with the same complaint — that rolls are somehow repeating themselves too frequently be truly random. So I wonder if there might be a glitch — not in the theoretical math of course, or even in the Java Random Number generator — but possibly in the interface between the sending of the dice roll data to the game itself. I’m not an IT guy at all, so I can only speculate.
I’m on an iMAC with Big Sur 11 and I’ve noticed that older generation websites have loading difficulties, which are alleviated by refreshing the site. Could it be possible that the Java RNG is working fine, but that it may end up sending the same dice roll twice or 3 times because the game site is not responding and it refreshes which then resends the same data?
I’ve noticed it myself in the few games I’ve played.
-
@HOFfridge
Exactly! I’m feeling the same thing. It’s the sudden cluster of repetitions, like holding and pressing a key which repeats the letter. And as I wrote to Jeremy above, I wonder if it might be a loading problem or a resending the same data problem with the old website platform? -
@HOFfridge 1 in 36 - a 2.78% chance for any roll.
So the same exact roll happening 4 times in a row is a 0.0000595% chance - or 1 in 1,679,616
Not great odds… but we may have played enough APBAGO games to see it. lol
-
@tomfortas-0 Hi!
If what you are implying is happening, then HoF’s example:
53, 53, 53, 31, 53
would prove that it is not happening.
That 31 would not be there.
Let’s look at some random numbers using php’s random number generator, as I have it in front of me:
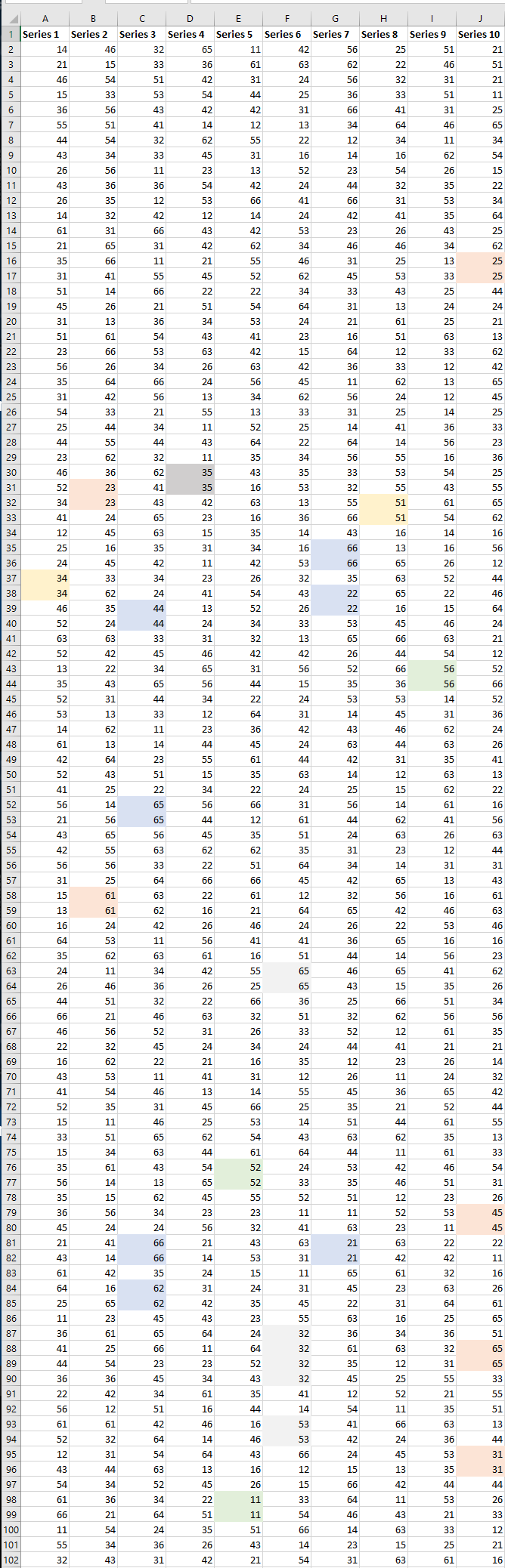
That’s 1,000 dice roles; 100 each for 10 managers.
Summary:
Manager number 6 looks to the sky, raises his fist and screams “Whhhhyyyyyyyyyyyyyyyy?!”
Unless that dice roll was a good result, for a favorite team, in which case there’s a lot of quiet chuckling.
Random will mess with your head… every time.
-
Here is a screenshot of my fielders turning into “the Three Stooges” or the Keystone Kops, whichever you prefer, with two out and the bases empty:
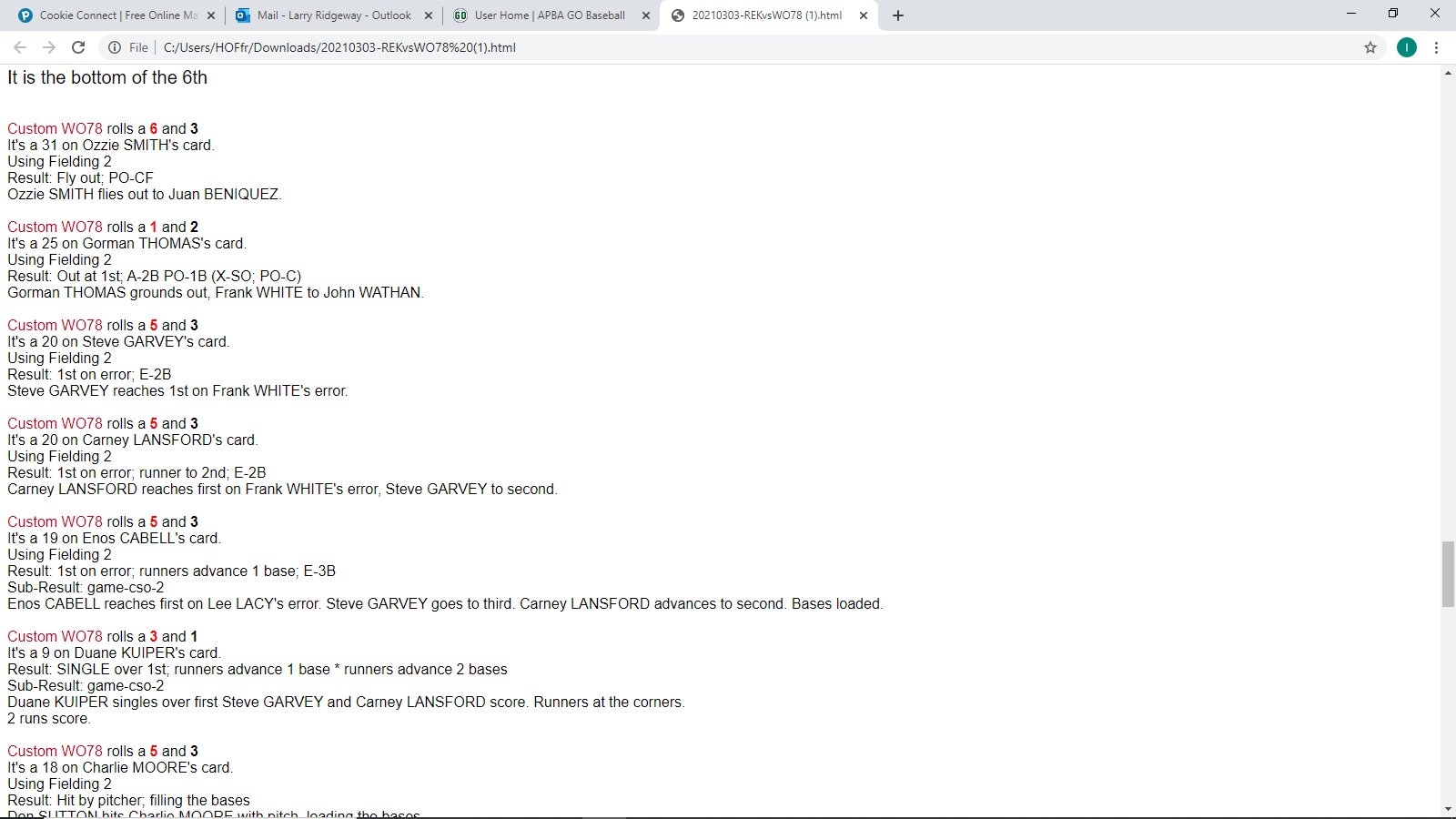
Note the fielder making the back to back errors is Frank White (2B-9).Not room to show the next batter, PH Frank Taveras with the 15-11 for the two-run single.
-
@APBA-GO-Jeremy
Yes, I hear you about HoF’s interrupted run of 4 53’s. And thank you for putting up that spreadsheet. It’s helping me scrape some rust off my long-neglected StatHead gears and made me realize that we are dealing with Conditional Probability in your chart of a thousand rolls whereas @HOFfridge is using Unconditional Probability to interpret his sequence of rolls.The difference is that you with the chart are tabulating the doubles that occur with any numbers on the dice. Whereas HOF is focused on only one number of the possible 36.
To give an example, if HOF predicts beforehand that he is going to roll a 53 twice, then that probability is 1/36 times 1/36 = 1/1296 or close to a “one in a thousand.”But you with the spreadsheet are tabulating Doubles that occur no matter what the number may be. In more StatSpeak, I would phrase it this way:
Given your prior knowledge of the first roll, what is the probability that the 2nd roll will duplicate the 1st roll?
For example, if you roll a 65, what is the probability that you will roll a 65 again? That probability will be 1/36.And that bears out on the spreadsheet. How many doubles should we expect in a thousand dice rolls?
1000 times 1/36 = 27.8
Let’s round up to 28.I count 21 Doubles on your spreadsheet, so, as the saying goes: “That’s close enough for government work!!”
I’m not sure how to handle a Triple, but I think your single Quadruple would be a 1 in 1296, i.e. one in a thousand. My reasoning is:
Given my prior knowledge of the Double 31, what is the probability of rolling another Double 31? That would be 1/36 times 1/36 = 1/1296. -
@tomfortas-0 Very cool analysis… ty!
-
I have mentioned it before, but I roll all my GO games manually. I still like the feel of the dice in my hand. That said, weird things happen.
I know for a fact I have rolled three 66’s in a row.
Just today, over a span of six batters, the 2014 Giants rolled two 66’s, two 33’s and one 11. (The 1917 White Sox Red Faber wasn’t too happy about it.) It happens.
And my all-time wild game took place last September (see below). It seemed like every other 1915 Phillies’ roll was either an 11, 22, 33 or 66. All while the 1991 Twins spent nine innings rolling duds.
If I hadn’t seen it with my own eyes, I’d have never believed it. Had this been an automated dice-roll game, I would have been certain something in the system was broken.
But all it really was… was one of those bizarre games. Whether the dice are manual or automated, crazy things are gonna happen…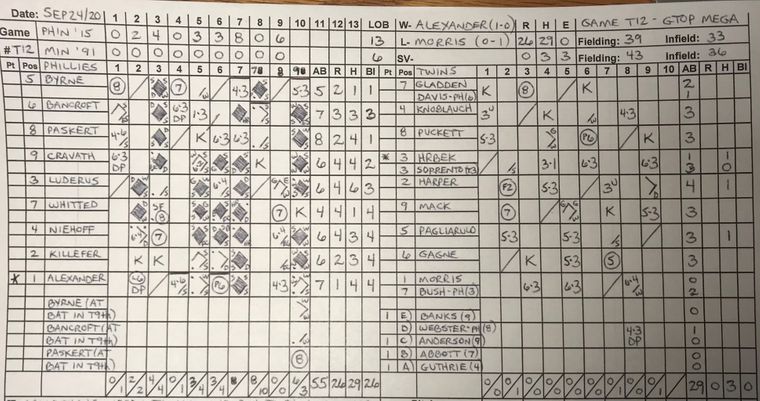
-
@APBA-GO-Jeremy People are very bad at detecting true randomness. When I use random number generators, I test millions of rolls for distribution of single numbers, repeat numbers, triply repeated numbers, and quadruply repeated numbers to make sure those fit expectations. The built-in random functions are very good nowadays.
And it’s very hard to convince users of that. :-)
Here’s an idea for revenue generation with APBA Go - offer new dice for $1! (Differently colored from the old dice, but powered by the same random number generator.) You’ll make a bundle!
